Structural Ramblings - D&D Cosmologies Pt. 1
One of the things regarding worldbuilding I have spent the most time on in recent years is Planar Cosmology. This aspect is touched on very little, but the geometric appeal and inherent complexity of the connections has attracted me for years. This post or series of posts will be agnostic to the actual playing of D&D or other RPG systems, and will simply talk about the lore and conceptual framework of Planes.
What is a plane?
I find it likely that the sort of people who would read this blog are already familiar with common fantasy RPG concepts such as planes, but I will give a quick definition here for those who aren't. The best analogy to a plane without leaning on fantasy tropes is that of Heaven and Hell. Those who believe in Heaven and Hell don't (usually) think that they are physical places in the universe as we know it. Even at infinite speed, you couldn't suddenly get there, as you could to another planet or galaxy. It is a place with specific characteristics, connected to our own plane only through some specific set of actions, not through usual motion. For those of you with a more mythological background, the Norse concept of 'Realms' is a good enough analog for planes.
The Traditional Planes

Above is an image of a traditional Forgotten Realms D&D planar cosmology. This is not the only one (there is a World Tree and World Axis model) but for our purposes this isn't necessary. This sort of Great Wheel cosmology is typically how the planes are shown. Here's an attempt at a quick overview of the structure of the planes.
At the center is the Material Plane. This is the normal world as you know it. Above and below this are the Feywild and Shadowfell, places that are similar and parallel to the Material Plane but with changes in specific vibe or elements (the Feywild being the chaotic home of Faeries, and the Shadowfell being dark and evil and ghostly). You can imagine them as funhouse mirror reflections of the Material Plane. Outside and in between these planes is the Ethereal Plane. This is a sort of ghostly, psychic soup that encompasses these planes. If each of these planes are islands, the Ethereal Plane is the ocean around them. Outwards of these planes are the Elemental Planes and Energy Planes. The Elemental Planes are the traditional four elements (Earth, Wind, Water, and Fire) in the natural opposition scheme you'd expect. The two Energy Planes are Positive (which can be thought of as Light) and Negative (which can be thought of as Darkness). These are all roughly in line with one another and have strong adjacencies (not shown in this map, which is one of my big problems with it showing the Energy Planes so far out). These adjacencies make up four Para-Elemental Planes, where two touching Elemental Planes meet. These are Smoke, Magma, Ooze, and Ice. There are also eight Quasi-Elemental Planes, meant to represent the borders between each of the four Elemental Planes and one of the two Energy Planes. These are Lightning, Steam, Radiance, Minerals, Vacuum, Salt, Ash, and Dust. In total, all of the things I've discussed to this point are part of what is known as the Inner Planes.
The Outer Planes are closer to our original Heaven and Hell analogy. They are planes where demons, angels, and other divine-esque creatures and gods live. In the traditional two-axes model, Up and Down represent Good and Evil, while Left and Right represent Law and Chaos.
Mapping out the Inner Planes.
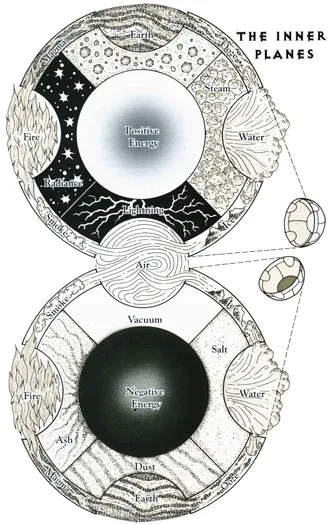
As you could probably tell from my explanation above, there is an incredible amount of implied complexity in the connections of the Inner Planes to each other that is just not shown at all in most maps and charts. Above is an image from the official Forgotten Realms Wiki that shows these connections, and is probably the clearest possible one to actually show off all Elemental, Energy, Para-, and Quasi-Elemental Planes. It does a pretty alright job. Many of the available diagrams or explanations are much worse, because they don't realize that these adjacencies only really map onto 3D, so your 2D representation has to be an unfolding of a 3D structure. Anyone who knows anything about map projections knows about this problem, but since adjacency is the only thing that really needs to be shown for these diagrams, the above split-sphere version is mostly fine. So, that's that, right?
A wrench in our Plan(e)s
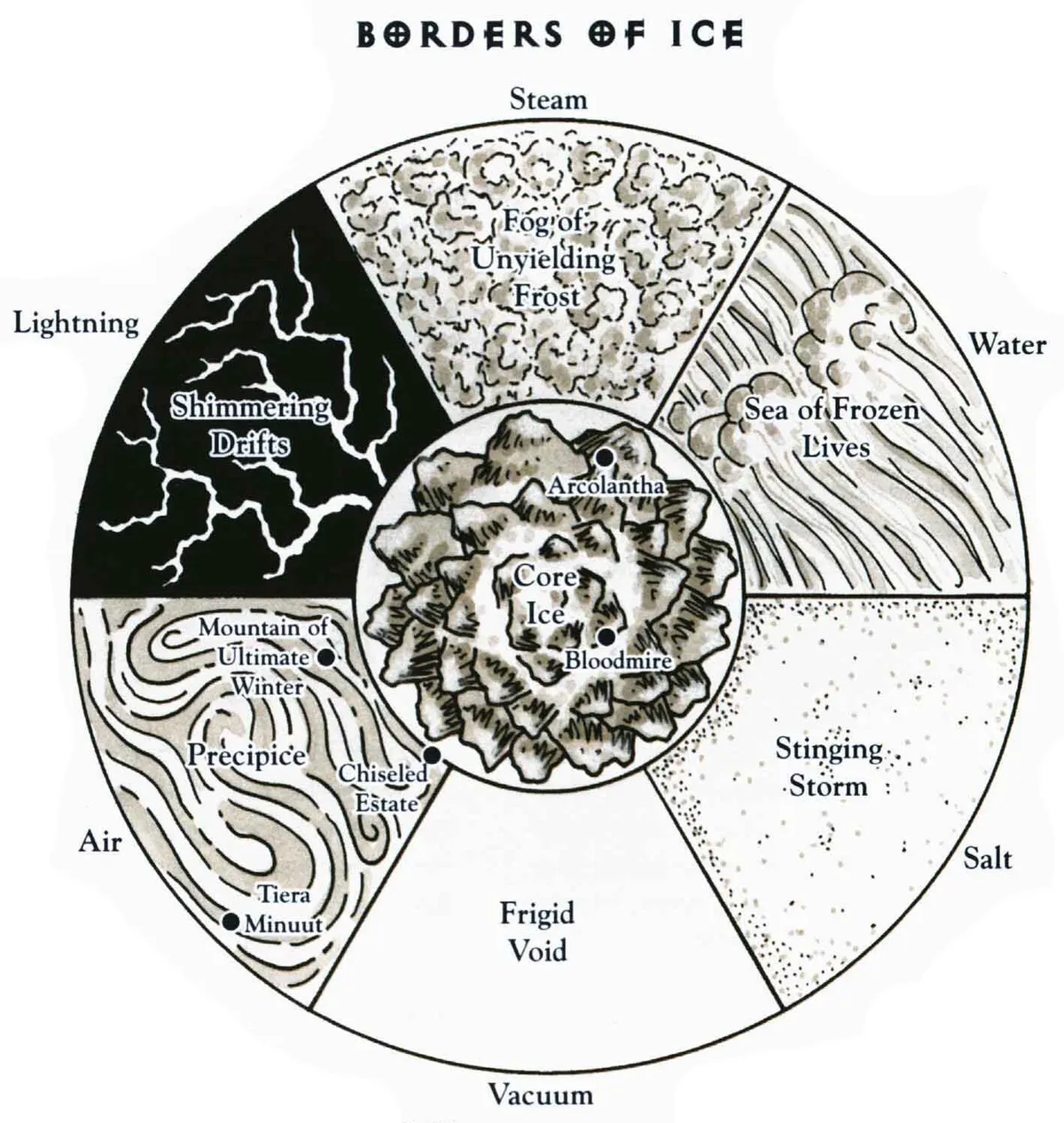
Not quite. The 1998 book The Inner Planes also diagrams out borders of all Para- and Quasi-Elemental Planes, exposing that the planes cannot be thought of as having a maximum of four adjacencies each, but rather six. Each Para-Elemental Plane connects not only to the two planes that make it up, but also to all four Quasi-Elemental Planes that come from them. Each Quasi-Elemental Plane connects not only to one Energy Plane and one Elemental Plane, but also to both the Para-Elemental Planes that come off of its main Elemental Plane and the two Quasi-Elemental Planes "next" to it.
Not only are there new connections, but the connections have specific names and characteristics. Also, sometimes, as per The Inner Planes, these connections are not commutative. So, going from Plane X to Plane Y you go through Subregion A, but going from Plane Y to Plane X you go through Subregion B. This essentially ruins the resolution of the original split-sphere model of the Inner Planes.
A fix?
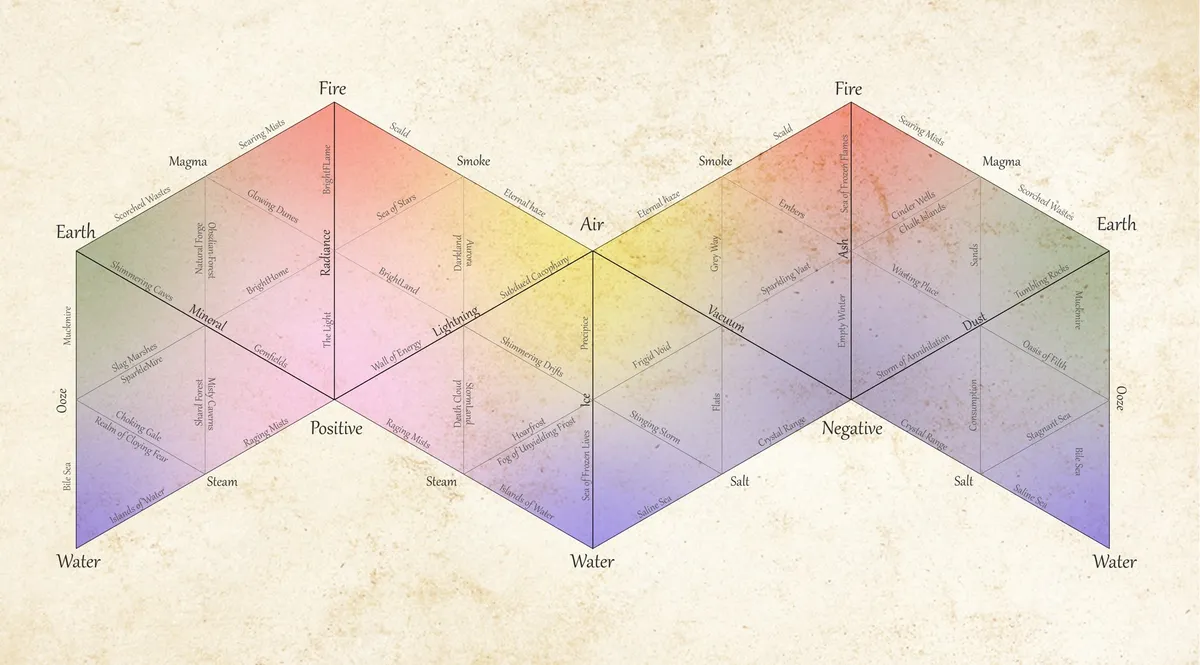
So I did it myself. It was quite simple actually, it just required modeling out the Elemental and Energy Planes as an eight-sided polygon, and then placing all the Quasi- and Para-Elemental Planes as the midpoints on their appropriate vertices. Then, the subregions could be labeled as individual vertices. This results in a 3D shape, which while accurate is not a useful map. I spoke earlier about normal map projections, which have to deal with turning a 3D model into a 2D image, and how this can be very hard due to distortions. But since I've modeled this as a polygon, we can simply unfold the polygon into a net of our choosing and make sure to label the points and vertices. I dealt with the non-commutative traveling issue by putting them on opposite sides of the vertex. Simply orient your origin plane as being on the left, your target point as being on the right, and in cases where there are two possible planes, the one above the line connecting them is the subregion you will go through. As far as I know, this is the first image that actually attempts to label the Inner Planes and their subregions on an accurate map (probably because the only time these subregions are brought up is in a 1998 bonus book).
Current Conclusion
This is a representation of only the start of my planar cosmology journey. I've never been a fan of just taking the content as-is and not changing it, so my next steps included adding some elements of my own (or ones I stole and synthesized from other sources). In future parts, we’ll touch on how that process is going.